理解RoPE位置嵌入

理解RoPE位置嵌入

ZYX
  2025-09-11 11:25:56 2025-09-11 11:25:56 Created   2025-09-11 11:25:56 2025-09-11 11:25:56 Updated  

大语言模型的第一步就是将数据处理成可以输入大模型的形式，即输入嵌入。这包含几个步骤，分别是：

  1. 使用分词器（如BPE）将输入文本划分为token
  2. 根据分词器的划分，构建token到token ID的双向映射
  3. 通过嵌入层，将token ID转换为嵌入向量（称为词元嵌入）
  4. 根据token在序列中的位置，创建位置嵌入
  5. 将3、4步得到的嵌入相加，得到输入大模型的输入嵌入
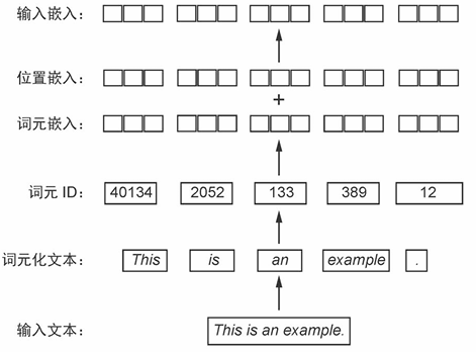
数据预处理过程

其他几个步骤都比较简单易懂，而步骤4中的创建位置嵌入则相对抽象一些。加入位置嵌入旨在为输入序列中的token添加位置信息。

传统的创建位置嵌入的方法可以分为绝对位置嵌入（Absolute Positional Embeddings）和相对位置（Relative Positional Embeddings）嵌入。近些年新出的大模型则更多采用RoPE（Rotary Positional Embeddings）位置嵌入。接下来将简单了解绝对位置嵌入和相对位置嵌入，然后具体理解一下RoPE的原理和实现方法。

论文地址：Arxiv PDF

绝对位置嵌入

假设我们有一个表示句子中一个token的嵌入，为了表示其位置信息，我们设置一个与该token相同维度的位置嵌入。因此该句子中的每一个token都可以有一个与之对应的相同维度的位置嵌入。将两者相加，便可以得到输入给大模型的输入嵌入。

绝对位置嵌入

绝对位置嵌入中位置嵌入主要有两种方法得到：1）从数据中学习 2）sin函数 具体实现方法暂时没有去了解。

绝对位置嵌入的第一个缺点是，输入嵌入的长度受到位置嵌入数量的限制，例如设置了512个位置嵌入，则输入嵌入的最大长度也为512。

绝对位置嵌入的第二个缺点是，位置向量彼此之间是完全独立的。例如，假设表示第i个位置的位置向量表示为pi，那么p1和p2之间与p2和p500之间实际上没有任何差别。但从直觉上将，我们认为p1和p2之间应该比p2和p500之间更相似。

相对位置嵌入

相对位置嵌入的思想是不表示token在句子中的绝对位置，而是学习句子中每对token的表示。很明显，每一对token的位置嵌入都不一样，所以我们不能简单地在词元嵌入上加一个位置嵌入。

正确的做法是修改注意力机制来增加相对位置嵌入。例如T5模型采用的相对位置编码方法是设置一个bias矩阵，由一系列浮点数组成，其中的元素bi表示输入序列中距离为i的token之间的相对距离。将该矩阵加到Self-Attention机制中的QK点积中

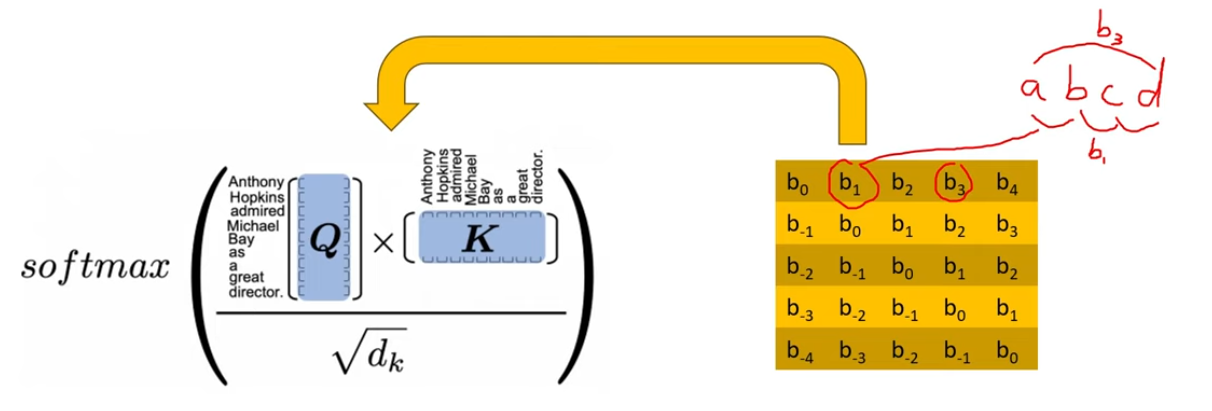
相对位置嵌入

这种做法的好处是相对距离相同的两个tokens都由相同的bias表示，无论它们在句子中所处的绝对位置。同时，这种方法可以扩展到任意长的序列当中。

这种方法的缺陷是速度十分慢，尤其是在长序列当中，这是因为相对位置嵌入需要在Self-Attention层中增加一个额外的步骤，即，将位置矩阵加到QK点积矩阵中，这种修改对于KV cache的利用率也有影响。因此在实际工程中的应用受到了限制。

RoPE

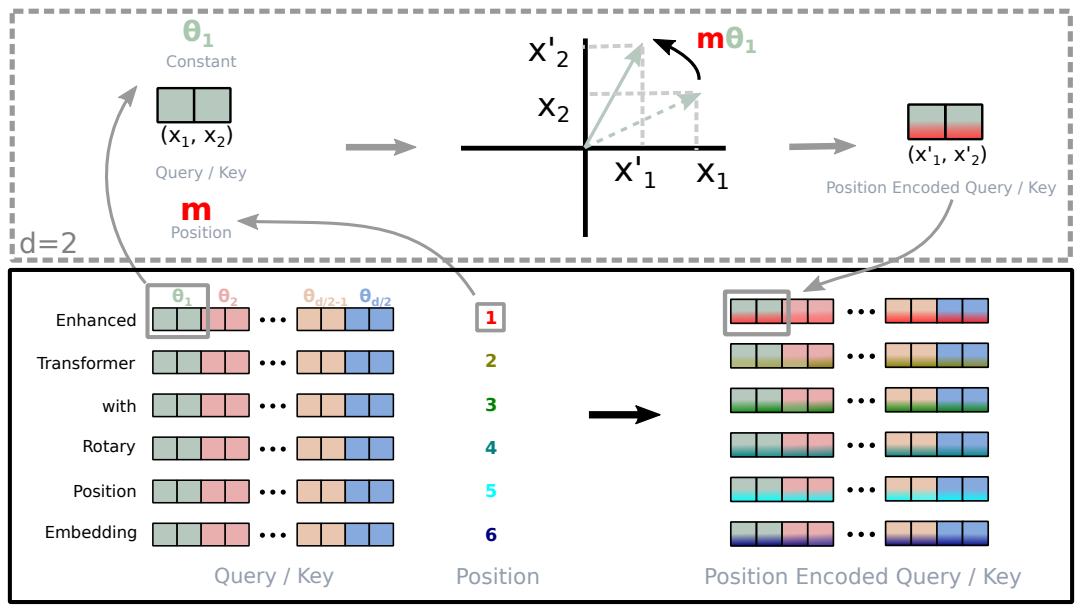
RoPE的核心思想不是增加一个位置向量来编码各个token的位置，而是提出了一种对向量进行旋转的方法。

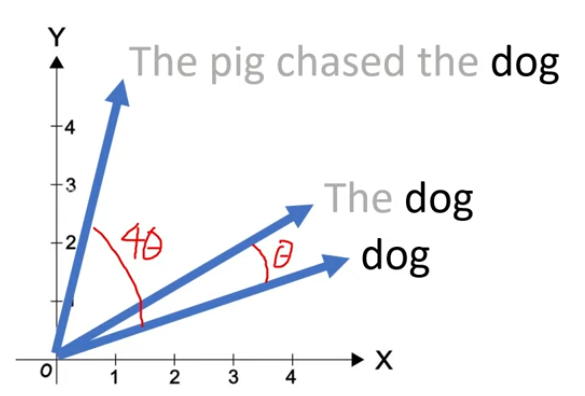
旋转一个token

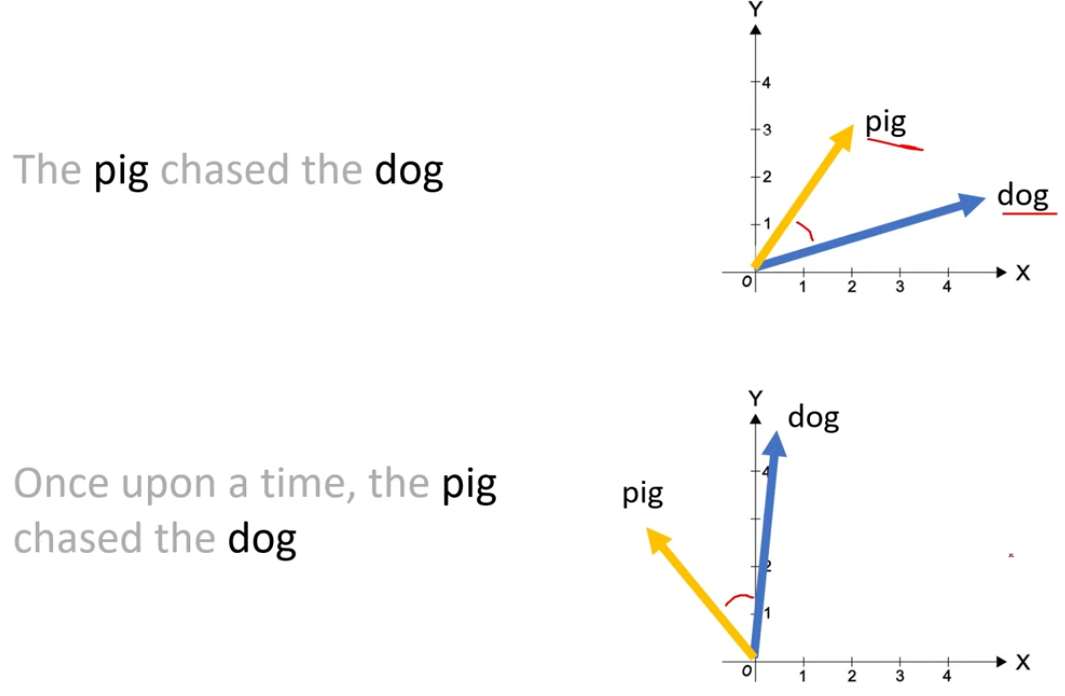
如图所示，假设有一个二维词向量表示dog，然后为了表示出现在第二个位置的dog，可以将这个向量旋转θ角度；为了表示出现在第5个位置的dog，可以将这个向量旋转5θ角度。这样无论dog出现在句子中的哪个位置，都只需要旋转θ的整数倍角度。例如，为了表示出现在第m个位置的dog，可以将dog的向量旋转mθ角度。

这种方式的好处之一是，在后续增加token时，例如在The dog后面无论继续增加多少token，前面的The和dog的位置向量表示不会受影响，这对cache来说是有益处的。（绝对位置编码的好处）

另一个好处是，向量之间的相对位置得到了保留。如图所示，原本pig和dog的位置向量相差3个位置，如上图所示，后续在前面加了一些tokens，导致pig和dog在句子中的绝对位置变化，但两者的相对位置没有改变，这可以通过同时旋转pig和dog相同角度来实现，最终两个向量之间的角度不变。也就是说当我们在前面或后面增加token的时候，只要两者的距离不变，则两者的点积保持不变。（相对位置编码的好处）

旋转两个token

RoPE的实现

以论文中提到的2维情况下的RoPE公式为例：

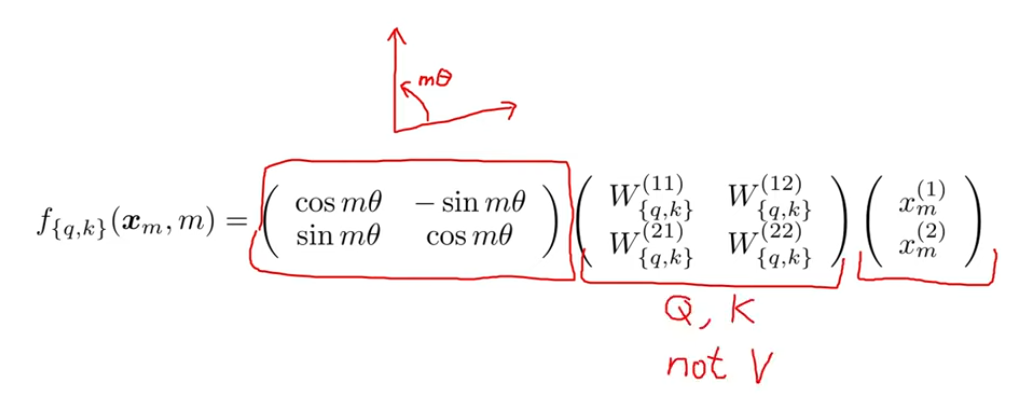
2维情况下RoPE的旋转公式

公式中最重要的部分是旋转矩阵，该矩阵的用处是将向量旋转mθ个角度，其中m表示token在句子中的绝对位置。x表示我们尝试旋转的向量，这里是2维的。在应用RoPE旋转之前，应当先用Q或者K矩阵对x进行线性变换，来得到query和key向量（只对query和key做旋转，不对value做）。

对于多于2维的情况，通常的做法是将向量切分成一个个2维的区块，然后按照2维的方法旋转它们。

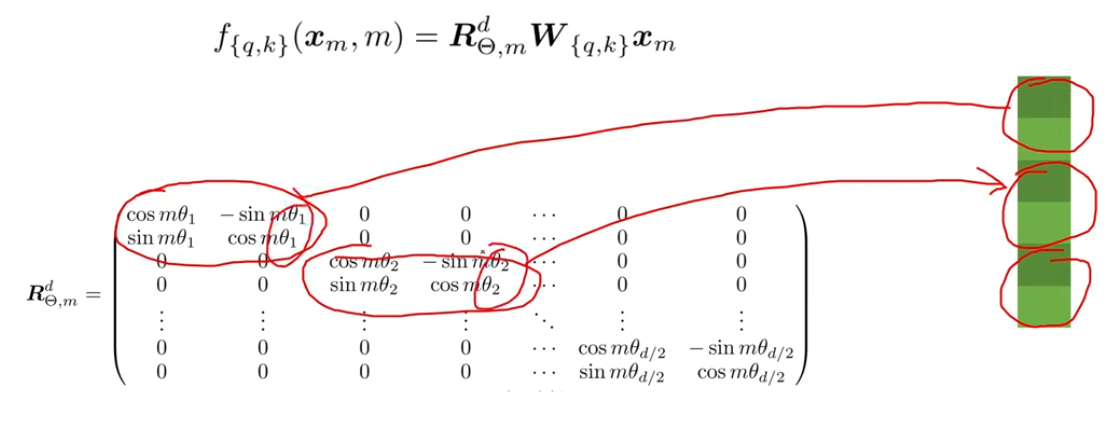
多维情况下RoPE的旋转公式

注意，这里的每一个区块都用不同的θ角度来旋转。另外，总是假设向量是偶数维度的。

RoPE的实际实现方法：

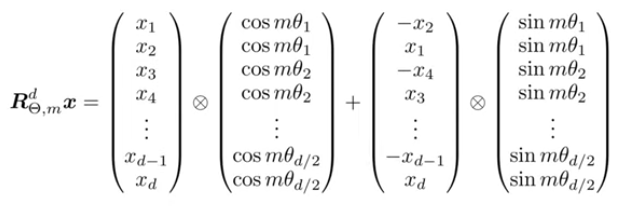
RoPE的实际实现方法

RoPE的代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
class RoPE(nn.Module):
    """
    Args:
        d_k (int): 注意力头的维度 (head dimension)。必须是偶数。
        theta (float): 用于计算旋转频率的基数。通常设置为 10000.0。
        max_seq_len (int): 模型支持的最大序列长度，用于预计算。
    """
    def __init__(self, d_k: int, theta: float = 10000.0, max_seq_len: int = 4096):
        super().__init__()
        
        if d_k % 2 != 0:
            raise ValueError(f"d_k 必须是偶数，但传入的是 {d_k}")

        self.d_k = d_k
        self.theta = theta
        self.max_seq_len = max_seq_len

        # 计算频率，缓存的维度是 [max_seq_len, d_k / 2]
        # 形状: [d_k / 2]
        inv_freq = 1.0 / (theta ** (torch.arange(0, d_k, 2).float() / d_k))
        
        # 形状: [max_seq_len]
        t = torch.arange(max_seq_len, dtype=inv_freq.dtype)

        # 形状: [max_seq_len, d_k / 2]
        freqs = torch.einsum("i,j->ij", t, inv_freq)

        # 缓存 cos 和 sin 值，注意这里的维度是 d_k / 2
        # 形状: [max_seq_len, d_k / 2]
        self.register_buffer("cos_cached", freqs.cos(), persistent=False)
        self.register_buffer("sin_cached", freqs.sin(), persistent=False)

    def forward(self, x: torch.Tensor, token_positions: torch.Tensor) -> torch.Tensor:
        """
        向前传播函数，对输入张量 x 应用旋转位置编码。
        Args:
            x (torch.Tensor): 输入张量，例如 Query 或 Key。
                              形状: Float[..., sequence_length, d_k] or [..., sequence_length, num_heads, d_k]
            token_positions (torch.Tensor): 每个 token 在序列中的绝对位置。
                                            形状: Int[..., sequence_length]
        Returns:
            torch.Tensor: 应用了 RoPE 后的张量，形状与 x 相同。
        """
        # 检查 token_positions 的范围
        if torch.max(token_positions) >= self.max_seq_len or torch.min(token_positions) < 0:
            raise ValueError(
                f"token_positions 中的值必须在 [0, {self.max_seq_len - 1}] 范围内。"
            )
    
        # 1. 提取对应位置的 cos 和 sin 值
        # cos/sin 形状: [batch_size, sequence_length, d_k/2]
        cos = self.cos_cached[token_positions]  # [batch_size, sequence_length, d_k/2]
        sin = self.sin_cached[token_positions]  # [batch_size, sequence_length, d_k/2]
    
        # 如果 x 包含 num_heads 维度，调整 cos 和 sin 的形状
        if x.dim() == 4:  # x shape: [batch_size, sequence_length, num_heads, d_k]
            # 扩展 cos 和 sin 以匹配 num_heads 维度
            cos = cos.unsqueeze(2)  # [batch_size, sequence_length, 1, d_k/2]
            sin = sin.unsqueeze(2)  # [batch_size, sequence_length, 1, d_k/2]
            cos = cos.expand(-1, -1, x.shape[2], -1)  # [batch_size, sequence_length, num_heads, d_k/2]
            sin = sin.expand(-1, -1, x.shape[2], -1)  # [batch_size, sequence_length, num_heads, d_k/2]
    
        # 2. 将输入张量 x 的最后一个维度看作是 d_k/2 个二维向量
        # 原始 x 形状: [..., sequence_length, d_k] 或 [..., sequence_length, num_heads, d_k]
        # reshape 后 x_reshaped 形状: [..., sequence_length, (num_heads), d_k/2, 2]
        x_reshaped = x.float().reshape(*x.shape[:-1], -1, 2)
    
        # 3. 分离出成对的元素 (x_i, x_{i+1})
        # x1, x2 形状: [..., sequence_length, (num_heads), d_k/2]
        x1, x2 = x_reshaped.unbind(-1)
    
        # 4. 应用旋转公式
        # x_out1 = x1 * cos - x2 * sin
        # x_out2 = x1 * sin + x2 * cos
        x_out1 = x1 * cos - x2 * sin
        x_out2 = x1 * sin + x2 * cos
    
        # 5. 将旋转后的对重新组合
        # 形状: [..., sequence_length, (num_heads), d_k/2, 2]
        x_rotated = torch.stack((x_out1, x_out2), dim=-1)
    
        # 6. 恢复张量的原始形状
        # 形状: [..., sequence_length, d_k] 或 [..., sequence_length, num_heads, d_k]
        return x_rotated.flatten(start_dim=-2)

RoPE的另一个好处是，在句子中相距较近的token具有较大的内积，而相距较远的token具有较小的内积。这也解决了绝对位置嵌入的第二个缺点。

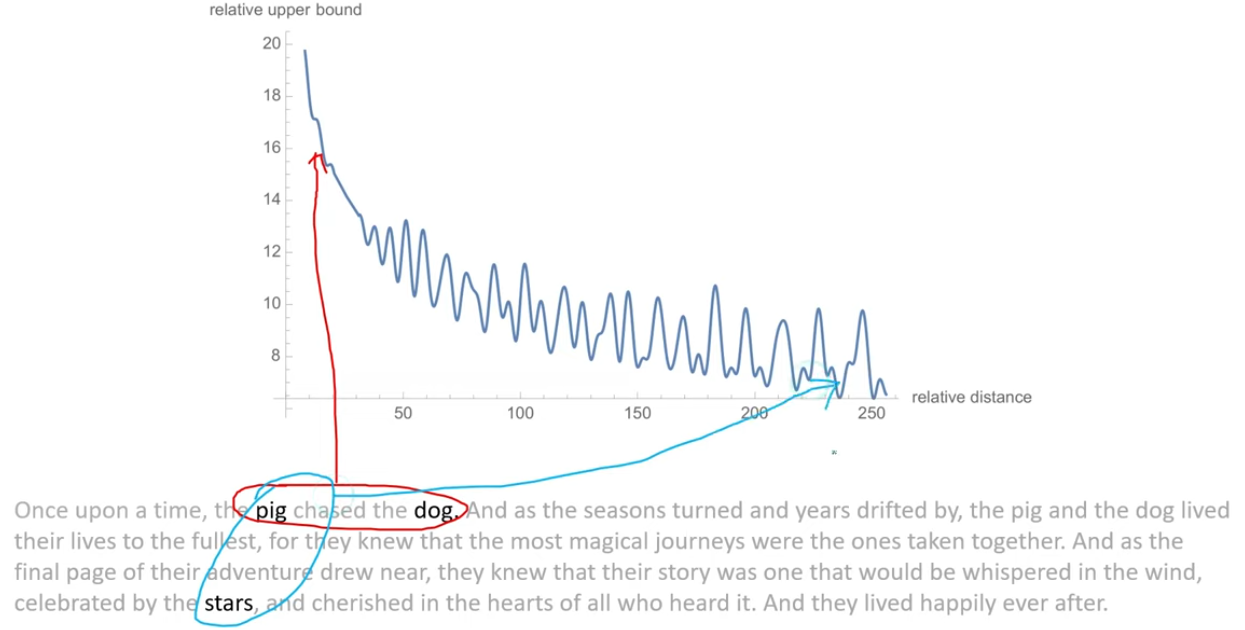
RoPE的另一个好处

经过很多模型的验证，RoPE的表现的确优于传统的绝对位置嵌入和相对位置嵌入。

  • Title: 理解RoPE位置嵌入
  • Author: ZYX
  • Created at : 2025-09-11 11:25:56
  • Updated at : 2025-09-11 11:25:56
  • Link: https://zyxzyx.top/理解RoPE位置嵌入/
  • License: This work is licensed under CC BY-NC-SA 4.0.
On this page
理解RoPE位置嵌入
  1. 绝对位置嵌入
  2. 相对位置嵌入
  3. RoPE
  4. RoPE的实现